در مقاله قبلی با الگوریتم جستجوی سطح اول آشنا شدیم که با کمک میکرد در یک گراف هم وزن مسیریابی کنیم، اما جستجوی سطح اول، در گراف های غیر هم وزن کاربردی ندارد. برای مثال اگر بخواهیم از یک نقطه از نقشه، به نقطه دیگری سفر کنیم، طول خیابان ها و جاده ها، یکسان نخواهد بود، پس ما به یک الگوریتم مسیریابی دیگر نیاز داریم که برای گراف های غیر هم وزن هم کار کند.
الگوریتم دیکسترا Dijkstra چیست و چه کاربردی دارد؟
الگوریتم دیکسترا، برای پیدا کردن کوتاه ترین مسیر استفاده میشود و در گراف های غیر هم وزن هم کاربرد دارد، این الگوریتم، یکی از الگوریتم های پایه ای در علوم کامپیوتر است و نام گذاری آن، به نام دانشمند هلندی است که این الگوریتم را برای اولین بار، ارائه داد.
هرچند این الگوریتم، برای پیدا کردن کوتاه ترین مسیر در گراف استفاده میشود، اما به این معنی نیست که فقط در نرم افزار های مسیریابی کاربرد دارد، این الگوریتم در شبکه و هوش مصنوعی هم کاربرد فراوانی دارد.
الگوریتم دیکسترا چطور کار میکند؟
الگوریتم دیکسترا، از چند مرحله بسیار ساده تشکیل شده است، در شروع کار، ما باید یک جدول طراحی کنیم و مدت زمانی که برای رسیدن به هر راس از گراف ، لازم است را در آن مینویسیم، در ابتدا که هنوز این اعداد محاسبه نشده برای راس مبدا، عدد صفر را قرار میدهیم و برای بقیه راس ها، بینهایت میگذاریم، سپس باید مراحل زیر را، تا جایی تکرار کنیم که همه راس ها را محاسبه کنیم.
- پیدا کردن نزدیک ترین راس؛ نزدیک ترین راسی که در حال حاضر، میتوانیم به آنجا برویم را پیدا میکنیم.
- از این راس به کدام راس ها میتوان رفت؟ اعدادی که در جدول، برای آن راس ها در نظر گرفتیم باید به روز شود.
- همین کار را تا جایی تکرار میکنیم که همه راس ها را، محاسبه کنیم و بتوانیم مسیر نهایی را محاسبه کنیم.
در شروع کار نزدیک ترین نقطه ای که میتوانیم برویم، همان نقطه مبدا است و باید اعداد مربوط به همسایه های آن را تغییر دهیم، همچنین باید توجه داشته باشیم که این عملیات را برای هر راس، فقط یک بار انجام بدهیم.
مثالی برای درک بهتر
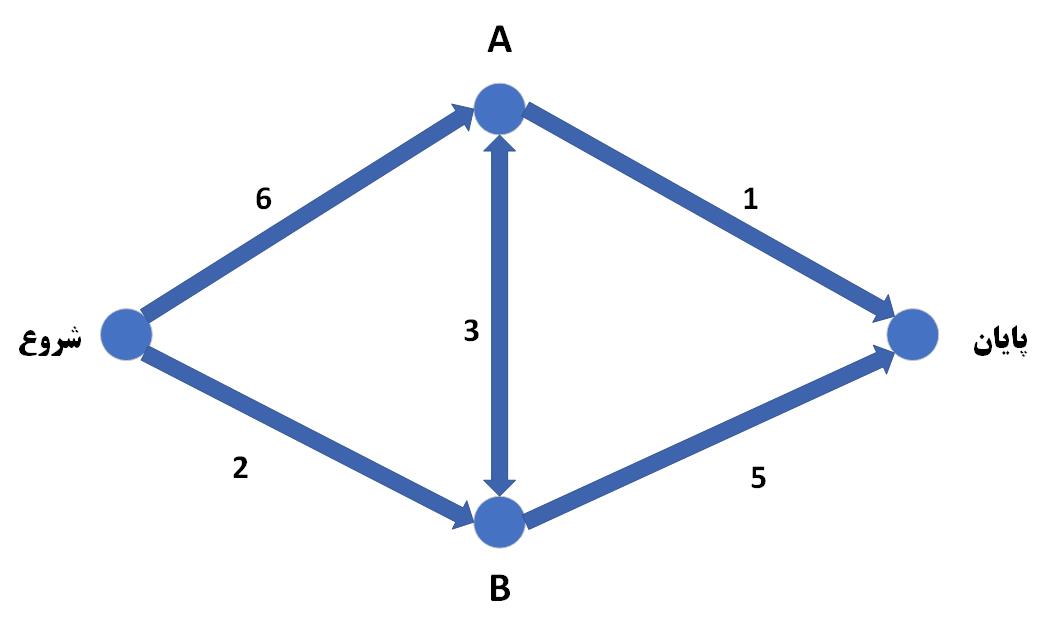
ما میخواهیم با استفاده از الگوریتم دیکسترا، سریع ترین مسیر، بین نقطه شروع و پایان، در نقشه بالا را پیدا کنیم، مرحله اول این است که همه راس ها را، در یک جدول قرار دهیم تا بتوانیم زمان رسیدن به هر یک را، محاسبه کنیم.
| صفر دقیقه | نقطه شروع |
| بی نهایت | نقطه A |
| بی نهایت | نقطه B |
| بی نهایت | نقطه پایان |
در ابتدا که اعداد را، محاسبه نکرده ایم عدد بی نهایت را قرار میدهیم و فقط نقطه شروع را صفر قرار میدهیم، سپس شروع میکنیم به تکرار سه مرحله که در بالا اشاره کردیم. مرحله اول پیدا کردن نزدیک ترین راس؛ در حال حاضر نزدیک ترین راس همان نقطه شروع است، مرحله دوم این است که اعداد مربوط به همسایه های این راس، را تغییر دهیم، از نقطه شروع متیوانیم با دو دقیقه زمان، به نقطه B برسیم و با 6 دقیقه زمان به نقطه A برسیم، پس جدول ما به صورت زیر خواهد شد.
| صفر دقیقه | نقطه شروع |
| 6 دقیقه | نقطه A |
| 2 دقیقه | نقطه B |
| بی نهایت | نقطه پایان |
حالا باید همین مراحل را، دوباره تکرار کنیم این باز نزدیک ترین راس، نقطه B خواهد بود، از این نقطه میتوانیم به نقطه A و نقطه پایان، سفر کنیم، برای رسیدن از نقطه B به نقطه A سه دقیقه زمان لازم است، و دو دقیقه زمان هم برای رسیدن به نقطه B، پس با استفاده از این راه جدید ما میتوانیم در عرض پنج دقیقه به نقطه A، برسیم. جدول جدید پس محاسبه اطلاعات مربوط به نقطه B، به صورت زیر خواهد شد.
| صفر دقیقه | نقطه شروع |
| 5 دقیقه | نقطه A |
| 2 دقیقه | نقطه B |
| 7 دقیقه | نقطه پایان |
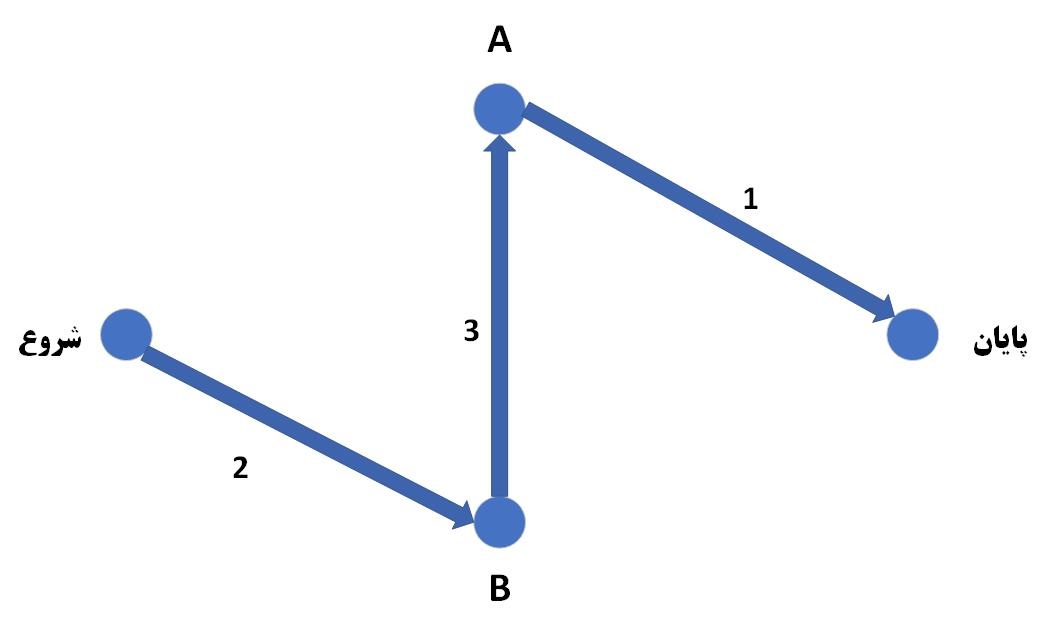
مجددا باید مراحل را تکرار کنیم، نزدیک ترین راسی که میتوانیم به آن برویم، نقطه A است (نقطه شروع و نقطه B، قبلا بررسی شده است). از نقطه A، میتوانیم با صرف کردن یک دقیقه به نقطه پایان برسیم، بنابرین ما میتوانیم در مجموع با شش دقیقه زمان، از نقطه شروع به نقطه پایان برسیم و مسیر نهایی به این صورت خواهد بود.
مقایسه الگوریتم دیکسترا و BFS
در این مقاله با الگوریتم دیکسترا، آشنا شدیم و در مقاله قبلی با الگوریتم دیگری به نام “الگوریتم جستجوی سطح اول” آشنا شده بودیم که از آن هم برای مسیریابی استفاده میکردیم، اما تفاوت این دو الگوریتم در کجاست؟ یکی از مهم ترین تفاوت ها این است که الگوریتم دیکسترا، برای گراف های غیر هم وزن هم کاربرد دارد، در صورتی که، جستجوی سطح اول، فقط برای گراف های هم وزن کاربرد دارد، همچنین الگوریتم دیکسترا سرعت بیشتری هم نسبت به الگوریتم جستجوی سطح اول دارد.
در مقابل الگوریتم جستجوی سطح اول، ساده تر است و به راحتی میتوان آن را پیاده سازی کرد و کاربرد آن محدود به الگوریتم های مسیریابی نمیشود و در مواردی دیگر مانند جستجو در گراف استفاده میشود.
جمع بندی
در این مقاله با الگوریتم دیکسترا، آشنا شدیم و یاد گرفتیم چطور از آن برای مسیریابی در گراف غیر هم وزن استفاده کنیم اما باید حتما به این نکته توجه داشته باشیم که کاربرد الگوریتم دیکسترا، به نرم افزار های مسیریابی محدود نمیشود و در هوش مصنوعی، شبکه های اجتماعی و هر جای دیگری که با گراف سر و کار داشته باشیم، میتواند استفاده شود.
اگر این مطلب برایتان مفید بود، پیشنهاد میکنم سری مقالات الگوریتم و ساختمان داده را دنبال کنید.
خیلی ممنون از اینکه وقت گذاشتید و این مقاله رو مطالعه کردید، ممنون میشم نظرتون رو بهم بگید.